"There, it was noticed that to an observer within the warp-drive bubble, the backward and forward walls (along the direction of motion) look, respectively, like the horizon of a black hole and of a white hole.”
PHYSICAL REVIEW D 79, 124017 (2009
Semiclassical instability of dynamical warp drives
Stefano Finazzi,1,* Stefano Liberati,1,† and Carlos Barcelo´ 2,‡
It looks like Alcubierre and everyone after him made a really stupid math mistake that completely changes the superluminal warp drive horizon picture when done correctly.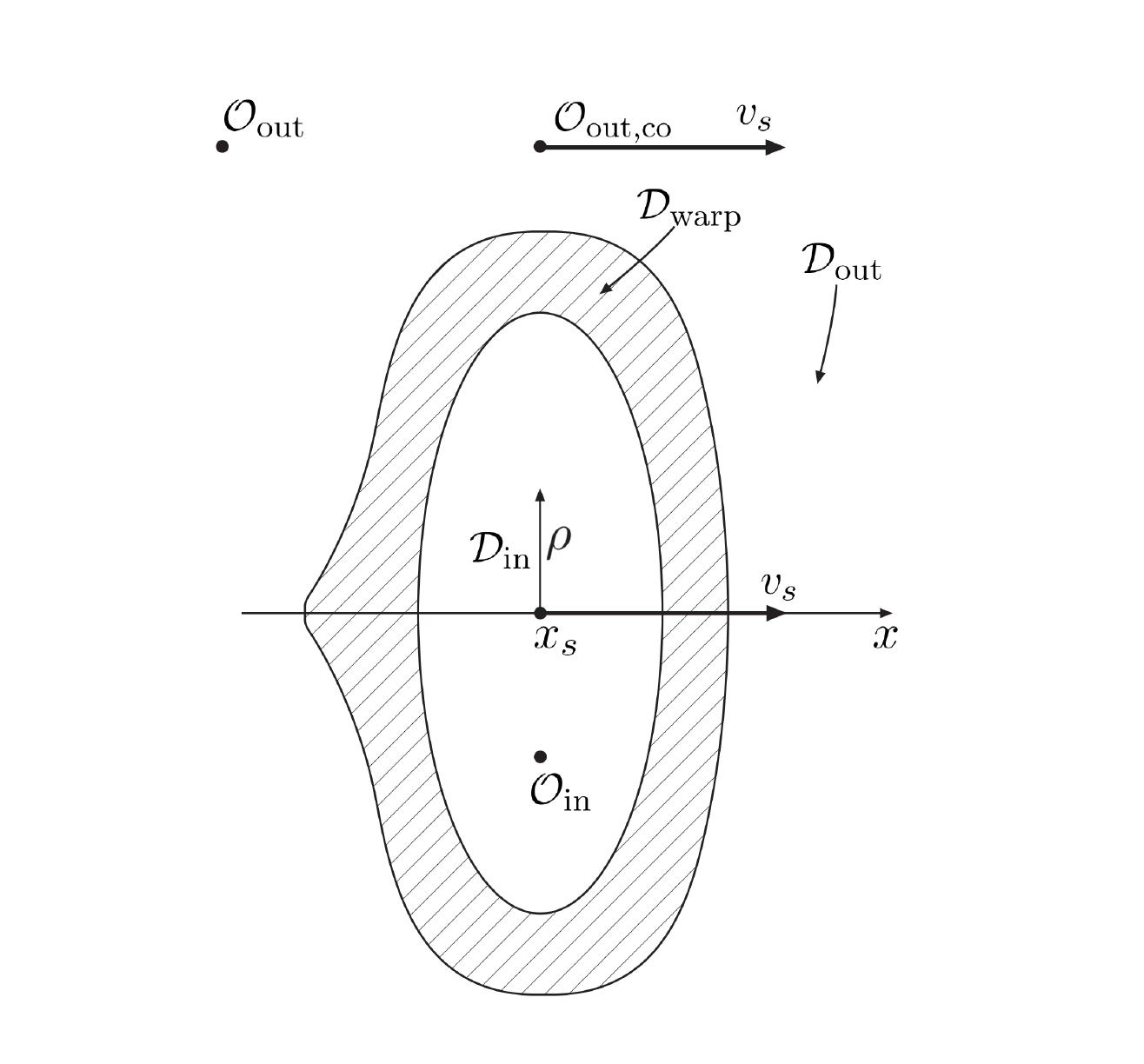

Introducing Physical Warp Drives
Alexey Bobrick, Gianni Martire
Advanced Propulsion
They use Galilean transformation
dx’ = dx - vdt
In transforming from the warp bubble rest frame to the observer frame outside the warp bubble and then take v > c.
This is clearly inconsistent.
In the simple 1 + 1 ST case
It’s only because they use the Galilean transformation that they get superluminal horizons
g00 = 0
From
g00 = (c + v)(c - v)
The metric inside the Tic Tac warp bubble Oin = Oout,cois simply the flat
ds^2 = -c^2dt’2 + dx’^2
Because the warp shape function f(r) = 1 and v = 0 in the rest frame of the Tic Tac.
Therefore, what Cmndr Fravor Oout sees outside the warp bubble must use the Lorentz transformations
dt' = (1 - (v/c)^2)^-1/2 [dt - (v/c^2)dx^2]
dx' = (1 - (v/c)^2)^-1/2 [dx - vdt]
ds^2 = - c^2 {(1 - (v/c)^2)^-1/2 [dt - (v/c^2)dx^2]}^2 + {(1 - (v/c)^2)^-1/2 [dx - vdt]}^2
= - c^2 (1 - (v/c)^2)^-1 [dt - (v/c^2)dx^2]^2 + (1 - (v/c)^2)^-1 [dx - vdt]^2
g00 = - (1 - (v/c)^2)^-1{- c^2 + v^2}
= - c^2
That is the time dilation and Lorentz contraction in the frame transformation from the interior to the exterior cancel out any horizons from the warp bubble. The apparent superluminal horizons are simply a false artifact from using the incorrect Galilean relativity transformation rather than the special relativity Lorentz transformation.
NO SUPERLUMINAL HORIZONS!
Check my algebra - did I make a mistake?
