Imagine an sender in spacetime region x and a receiver in spacetime region y. According to Feynman the partial retarded quantum amplitude A(x,y) for the signal to leave x in the past and arrive at y in the future along a definite path P is
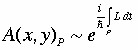
The integrand L in the phase of the exponential function is the classical Lagrangian, which in the simplest toy model of a single point particle is L = Kinetic Energy – Potential Energy with only conservative non-dissipative and non-velocity dependent forces. The infinitesimal segments of the signal’s path P are arbitrary even superluminal outside the local light cone. However, when one sums over the set of all possible paths {P} with the same end points x and y, assuming there is no way to distinguish the paths with intermediate measurements, the total amplitude connecting x and y is the coherent superposition of all the partial amplitudes
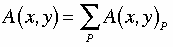
There will be at least one special path Pc along which the phases of the summed exponential functions constructively interfere, analogous to the maxima in an optical interference pattern, and this is the classical path predicted say by Newton’s mechanics in the simplest toy model where special relativity’s time dilation and length contraction are ignorable.
We now also assume that the Lagrangian L is invariant under time reversal t à-t = t’ keeping x and y fixed. Therefore, the advanced time-reversed amplitude A(y,x) summed over the time-reversed paths P’ is simply the complex-conjugate of the original amplitude. This advanced amplitude is literally back from the future receiver to the past emitter.
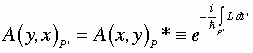
The Born probability conjecture is that the conditional probability P(x,y) for the signal to leave x in the past and arrive at y in the future is the modulation of the retarded total amplitude by the advanced total amplitude.
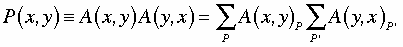
There are two kinds of terms in the double sum, diagonal where P = P’ corresponding to closed timeloops with zero area and off-diagonal interference terms P =/= P’ corresponding to closed time loops with finite area. It’s the latter finite area timeloops that are specifically quantum.
"In quantum mechanics and quantum field theory, the propagator gives the probability amplitude for a particle to travel from one place to another in a given time, or to travel with a certain energy and momentum. Propagators are used to represent the contribution of virtual particles on the internal lines of Feynman diagrams. They also can be viewed as the inverse of the wave operator appropriate to the particle, and are therefore often called Green's functions. ...
Faster than light?
The Feynman propagator has some properties that seem baffling at first. In particular, unlike the commutator, the propagator is nonzero outside of the light cone, though it falls off rapidly for spacelike intervals. Interpreted as an amplitude for particle motion, this translates to the virtual particle traveling faster than light. It is not immediately obvious how this can be reconciled with causality: can we use faster-than-light virtual particles to send faster-than-light messages?
The answer is no: while in classical mechanics the intervals along which particles and causal effects can travel are the same, this is no longer true in quantum field theory, where it is commutators that determine which operators can affect one another.
So what does the spacelike part of the propagator represent? In QFT the vacuum is an active participant, and particle numbers and field values are related by an uncertainty principle; field values are uncertain even for particle number zero. There is a nonzero probability amplitude to find a significant fluctuation in the vacuum value of the field Φ(x) if one measures it locally (or, to be more precise, if one measures an operator obtained by averaging the field over a small region). Furthermore, the dynamics of the fields tend to favor spatially correlated fluctuations to some extent. The nonzero time-ordered product for spacelike-separated fields then just measures the amplitude for a nonlocal correlation in these vacuum fluctuations, analogous to an EPR correlation. Indeed, the propagator is often called a two-point correlation function for the free field.
Since, by the postulates of quantum field theory, all observable operators commute with each other at spacelike separation, messages can no more be sent through these correlations than they can through any other EPR correlations; the correlations are in random variables.
In terms of virtual particles, the propagator at spacelike separation can be thought of as a means of calculating the amplitude for creating a virtual particle-antiparticle pair that eventually disappear into the vacuum, or for detecting a virtual pair emerging from the vacuum. In Feynman's language, such creation and annihilation processes are equivalent to a virtual particle wandering backward and forward through time, which can take it outside of the light cone. However, no causality violation is involved.
Propagators in Feynman diagrams
The most common use of the propagator is in calculating probability amplitudes for particle interactions using Feynman diagrams. These calculations are usually carried out in momentum space. In general, the amplitude gets a factor of the propagator for every internal line, that is, every line that does not represent an incoming or outgoing particle in the initial or final state. It will also get a factor proportional to, and similar in form to, an interaction term in the theory's Lagrangian for every internal vertex where lines meet. These prescriptions are known as Feynman rules.
Internal lines correspond to virtual particles. Since the propagator does not vanish for combinations of energy and momentum disallowed by the classical equations of motion, we say that the virtual particles are allowed to be off shell. In fact, since the propagator is obtained by inverting the wave equation, in general it will have singularities on shell.
The energy carried by the particle in the propagator can even be negative. This can be interpreted simply as the case in which, instead of a particle going one way, its antiparticle is going the other way, and therefore carrying an opposing flow of positive energy. The propagator encompasses both possibilities. It does mean that one has to be careful about minus signs for the case of fermions, whose propagators are not even functions in the energy and momentum (see below).
Virtual particles conserve energy and momentum. However, since they can be off shell, wherever the diagram contains a closed loop, the energies and momenta of the virtual particles participating in the loop will be partly unconstrained, since a change in a quantity for one particle in the loop can be balanced by an equal and opposite change in another. Therefore, every loop in a Feynman diagram requires an integral over a continuum of possible energies and momenta. In general, these integrals of products of propagators can diverge, a situation that must be handled by the process of renormalization." Wikipedia
"In quantum field theory, the statistical mechanics of fields, and the theory of self-similar geometric structures, renormalization refers to a collection of techniques used to take a continuum limit.
When describing space and time as a continuum, certain statistical and quantum mechanical constructions are ill defined. To define them, the continuum limit has to be taken carefully.
Renormalization determines the relationship between parameters in the theory, when the parameters describing large distance scales differ from the parameters describing small distances. Renormalization was first developed in quantum electrodynamics (QED) to make sense of infinite integrals in perturbation theory. Initially viewed as a suspicious, provisional procedure by some of its originators, renormalization eventually was embraced as an important and self-consistent tool in several fields of physics and mathematics. ...
The total effective mass of a spherical charged particle includes the actual bare mass of the spherical shell (in addition to the aforementioned mass associated with its electric field). If the shell's bare mass is allowed to be negative, it might be possible to take a consistent point limit.[1] This was called renormalization, and Lorentz and Abraham attempted to develop a classical theory of the electron this way. This early work was the inspiration for later attempts at regularization and renormalization in quantum field theory.
When calculating the electromagnetic interactions of charged particles, it is tempting to ignore the back-reaction of a particle's own field on itself. But this back reaction is necessary to explain the friction on charged particles when they emit radiation. If the electron is assumed to be a point, the value of the back-reaction diverges, for the same reason that the mass diverges, because the field is inverse-square.
The Abraham-Lorentz theory had a noncausal "pre-acceleration". Sometimes an electron would start moving before the force is applied. This is a sign that the point limit is inconsistent. An extended body will start moving when a force is applied within one radius of the center of mass.
The trouble was worse in classical field theory than in quantum field theory, because in quantum field theory a charged particle experiences Zitterbewegung due to interference with virtual particle-antiparticle pairs, thus effectively smearing out the charge over a region comparable to the Compton wavelength. In quantum electrodynamics at small coupling the electromagnetic mass only diverges as the log of the radius of the particle. ...
The divergences appear in calculations involving Feynman diagrams with closed loops of virtual particles in them.
While virtual particles obey conservation of energy and momentum, they can have any energy and momentum, even one that is not allowed by the relativistic energy-momentum relation for the observed mass of that particle. (That is, E^2 − p^2 is not necessarily the squared rest mass of the particle in that process (e.g. for a photon it could be nonzero).) Such a particle is called off-shell. When there is a loop, the momentum of the particles involved in the loop is not uniquely determined by the energies and momenta of incoming and outgoing particles. A variation in the energy of one particle in the loop can be balanced by an equal and opposite variation in the energy of another particle in the loop. So to find the amplitude for the loop process one must integrate over all possible combinations of energy and momentum that could travel around the loop.
These integrals are often divergent, that is, they give infinite answers. The divergences which are significant are the "ultraviolet" (UV) ones. An ultraviolet divergence can be described as one which comes from the region in the integral where all particles in the loop have large energies and momenta. very short wavelengths and high frequencies fluctuations of the fields, in the path integral for the field. Very short proper-time between particle emission and absorption, if the loop is thought of as a sum over particle paths. So these divergences are short-distance, short-time phenomena.
There are exactly three one-loop divergent loop diagrams in quantum electrodynamics.
1) a photon creates a virtual electron-positron pair which then annihilate, this is a vacuum polarization diagram.
2) an electron which quickly emits and reabsorbs a virtual photon, called a self-energy.
3) An electron emits a photon, emits a second photon, and reabsorbs the first. This process is shown in figure 2, and it is called a vertex renormalization.
The three divergences correspond to the three parameters in the theory:
1') the field normalization Z.
2') the mass renormalization of the electron.
3') the charge renormalization of the electron.
A second class of divergence, called an infrared divergence, is due to massless particles, like the photon. Every process involving charged particles emits infinitely many coherent photons of infinite wavelength, and the amplitude for emitting any finite number of photons is zero. For photons, these divergences are well understood. For example, at the 1-loop order, the vertex function has both ultraviolet and infrared divergences. In contrast to the ultraviolet divergence, the infrared divergence does not require the renormalization of a parameter in the theory. The infrared divergence of the vertex diagram is removed by including a diagram similar to the vertex diagram with the following important difference: the photon connecting the two legs of the electron is cut and replaced by two on shell (i.e. real) photons whose wavelengths tend to infinity; this diagram is equivalent to the bremsstrahlung process. This additional diagram must be included because there is no physical way to distinguish a zero-energy photon flowing through a loop as in the vertex diagram and zero-energy photons emitted through bremsstrahlung. ...
The solution was to realize that the quantities initially appearing in the theory's formulae (such as the formula for the Lagrangian), representing such things as the electron's electric charge and mass, as well as the normalizations of the quantum fields themselves, did not actually correspond to the physical constants measured in the laboratory. As written, they were bare quantities that did not take into account the contribution of virtual-particle loop effects to the physical constants themselves. Among other things, these effects would include the quantum counterpart of the electromagnetic back-reaction that so vexed classical theorists of electromagnetism. In general, these effects would be just as divergent as the amplitudes under study in the first place; so finite measured quantities would in general imply divergent bare quantities.
In order to make contact with reality, then, the formulae would have to be rewritten in terms of measurable, renormalized quantities. The charge of the electron, say, would be defined in terms of a quantity measured at a specific kinematic renormalization point or subtraction point (which will generally have a characteristic energy, called the renormalization scale or simply the energy scale). The parts of the Lagrangian left over, involving the remaining portions of the bare quantities, could then be reinterpreted as counterterms, involved in divergent diagrams exactly canceling out the troublesome divergences for other diagrams. ...
Gauge invariance, via a Ward-Takahashi identity, turns out to imply that we can renormalize the two terms of the electromagnetic covariant derivative ...
The physical constant e, the electron's charge, can then be defined in terms of some specific experiment; we set the renormalization scale equal to the energy characteristic of this experiment, and the first term gives the interaction we see in the laboratory (up to small, finite corrections from loop diagrams, providing such exotica as the high-order corrections to the magnetic moment). The rest is the counterterm. If we are lucky, the divergent parts of loop diagrams can all be decomposed into pieces with three or fewer legs, with an algebraic form that can be canceled out by the second term (or by the similar counterterms that come from Z0 and Z3). In QED, we are lucky: the theory is renormalizable ...
The splitting of the "bare terms" into the original terms and counterterms came before the renormalization group insights due to Kenneth Wilson. According to the renormalization group insights, this splitting is unnatural and unphysical.
Running constants
To minimize the contribution of loop diagrams to a given calculation (and therefore make it easier to extract results), one chooses a renormalization point close to the energies and momenta actually exchanged in the interaction. However, the renormalization point is not itself a physical quantity: the physical predictions of the theory, calculated to all orders, should in principle be independent of the choice of renormalization point, as long as it is within the domain of application of the theory. Changes in renormalization scale will simply affect how much of a result comes from Feynman diagrams without loops, and how much comes from the leftover finite parts of loop diagrams. One can exploit this fact to calculate the effective variation of physical constants with changes in scale. This variation is encoded by beta-functions, and the general theory of this kind of scale-dependence is known as the renormalization group.
Colloquially, particle physicists often speak of certain physical constants as varying with the energy of an interaction, though in fact it is the renormalization scale that is the independent quantity. This running does, however, provide a convenient means of describing changes in the behavior of a field theory under changes in the energies involved in an interaction. For example, since the coupling constant in non-Abelian SU3 quantum chromodynamics becomes small at large energy scales, the theory behaves more like a free theory as the energy exchanged in an interaction becomes large, a phenomenon known as asymptotic freedom. Choosing an increasing energy scale and using the renormalization group makes this clear from simple Feynman diagrams; were this not done, the prediction would be the same, but would arise from complicated high-order cancellations. ...
Since the quantity "infinity - infinity" is ill-defined, in order to make this notion of canceling divergences precise, the divergences first have to be tamed mathematically using the theory of limits, in a process known as regularization.
An essentially arbitrary modification to the loop integrands, or regulator, can make them drop off faster at high energies and momenta, in such a manner that the integrals converge. A regulator has a characteristic energy scale known as the cutoff; taking this cutoff to infinity (or, equivalently, the corresponding length/time scale to zero) recovers the original integrals.
With the regulator in place, and a finite value for the cutoff, divergent terms in the integrals then turn into finite but cutoff-dependent terms. After canceling out these terms with the contributions from cutoff-dependent counterterms, the cutoff is taken to infinity and finite physical results recovered. If physics on scales we can measure is independent of what happens at the very shortest distance and time scales, then it should be possible to get cutoff-independent results for calculations. ...
Attitudes and interpretation
The early formulators of QED and other quantum field theories were, as a rule, dissatisfied with this state of affairs. It seemed illegitimate to do something tantamount to subtracting infinities from infinities to get finite answers.
Dirac's criticism was the most persistent. As late as 1975, he was saying:
Most physicists are very satisfied with the situation. They say: 'Quantum electrodynamics is a good theory and we do not have to worry about it any more.' I must say that I am very dissatisfied with the situation, because this so-called 'good theory' does involve neglecting infinities which appear in its equations, neglecting them in an arbitrary way. This is just not sensible mathematics. Sensible mathematics involves neglecting a quantity when it is small - not neglecting it just because it is infinitely great and you do not want it!
Another important critic was Feynman. Despite his crucial role in the development of quantum electrodynamics, he wrote the following in 1985:
The shell game that we play ... is technically called 'renormalization'. But no matter how clever the word, it is still what I would call a dippy process! Having to resort to such hocus-pocus has prevented us from proving that the theory of quantum electrodynamics is mathematically self-consistent. It's surprising that the theory still hasn't been proved self-consistent one way or the other by now; I suspect that renormalization is not mathematically legitimate.
While Dirac's criticism was based on the procedure of renormalization itself, Feynman's criticism was very different. Feynman was concerned that all field theories known in the 1960s had the property that the interactions becomes infinitely strong at short enough distance scales. This property, called a Landau pole, made it plausible that quantum field theories were all inconsistent. In 1974, Gross, Politzer and Wilczek showed that another quantum field theory, Quantum Chromodynamics, does not have a Landau pole. Feynman, along with most others, accepted that QCD was a fully consistent theory.
The general unease was almost universal in texts up to the 1970s and 1980s. Beginning in the 1970s, however, inspired by work on the renormalization group and effective field theory, and despite the fact that Dirac and various others—all of whom belonged to the older generation—never withdrew their criticisms, attitudes began to change, especially among younger theorists. Kenneth G. Wilson and others demonstrated that the renormalization group is useful in statistical field theory applied to condensed matter physics, where it provides important insights into the behavior of phase transitions. In condensed matter physics, a real short-distance regulator exists: matter ceases to be continuous on the scale of atoms. Short-distance divergences in condensed matter physics do not present a philosophical problem, since the field theory is only an effective, smoothed-out representation of the behavior of matter anyway; there are no infinities since the cutoff is actually always finite, and it makes perfect sense that the bare quantities are cutoff-dependent.
If QFT holds all the way down past the Planck length (where it might yield to string theory, causal set theory or something different), then there may be no real problem with short-distance divergences in particle physics either; all field theories could simply be effective field theories. In a sense, this approach echoes the older attitude that the divergences in QFT speak of human ignorance about the workings of nature, but also acknowledges that this ignorance can be quantified and that the resulting effective theories remain useful.
In QFT, the value of a physical constant, in general, depends on the scale that one chooses as the renormalization point, and it becomes very interesting to examine the renormalization group running of physical constants under changes in the energy scale. The coupling constants in the Standard Model of particle physics vary in different ways with increasing energy scale: the coupling of quantum chromodynamics and the weak isospin coupling of the electroweak force tend to decrease, and the weak hypercharge coupling of the electroweak force tends to increase. At the colossal energy scale of 10^15 GeV (far beyond the reach of our current particle accelerators), they all become approximately the same size (Grotz and Klapdor 1990, p. 254), a major motivation for speculations about grand unified theory. Instead of being only a worrisome problem, renormalization has become an important theoretical tool for studying the behavior of field theories in different regimes.
If a theory featuring renormalization (e.g. QED) can only be sensibly interpreted as an effective field theory, i.e. as an approximation reflecting human ignorance about the workings of nature, then the problem remains of discovering a more accurate theory that does not have these renormalization problems. As Lewis Ryder has put it, "In the Quantum Theory, these [classical] divergences do not disappear; on the contrary, they appear to get worse. And despite the comparative success of renormalisation theory the feeling remains that there ought to be a more satisfactory way of doing things."[4]
Renormalizability
From this philosophical reassessment a new concept follows naturally: the notion of renormalizability. Not all theories lend themselves to renormalization in the manner described above, with a finite supply of counterterms and all quantities becoming cutoff-independent at the end of the calculation. If the Lagrangian contains combinations of field operators of high enough dimension in energy units, the counterterms required to cancel all divergences proliferate to infinite number, and, at first glance, the theory would seem to gain an infinite number of free parameters and therefore lose all predictive power, becoming scientifically worthless. Such theories are called nonrenormalizable.
The Standard Model of particle physics contains only renormalizable operators, but the interactions of general relativity become nonrenormalizable operators if one attempts to construct a field theory of quantum gravity in the most straightforward manner, suggesting that perturbation theory is useless in application to quantum gravity."
[Sarfatti comment: The LIF spin 1 tetrad "Dirac square root" reformulation of Einstein's spin 2 metric tensor gravity may be renormalizable. In addition, the Penrose-Newman null tetrads are quadratic in advanced and retarded qubit light cone spinors. In contrast, the non-null LIF tetrads are simply the entangled Bell pair states of two spinor qubits. This formal correspondence of Penrose and Rindler seems the obvious implementation of John Archibald Wheeler's heuristic "IT FROM BIT"]
"However, in an effective field theory, "renormalizability" is, strictly speaking, a misnomer. In a nonrenormalizable effective field theory, terms in the Lagrangian do multiply to infinity, but have coefficients suppressed by ever-more-extreme inverse powers of the energy cutoff. If the cutoff is a real, physical quantity—if, that is, the theory is only an effective description of physics up to some maximum energy or minimum distance scale—then these extra terms could represent real physical interactions. Assuming that the dimensionless constants in the theory do not get too large, one can group calculations by inverse powers of the cutoff, and extract approximate predictions to finite order in the cutoff that still have a finite number of free parameters. It can even be useful to renormalize these "nonrenormalizable" interactions.
Nonrenormalizable interactions in effective field theories rapidly become weaker as the energy scale becomes much smaller than the cutoff. The classic example is the Fermi theory of the weak nuclear force, a nonrenormalizable effective theory whose cutoff is comparable to the mass of the W particle. This fact may also provide a possible explanation for why almost all of the particle interactions we see are describable by renormalizable theories. It may be that any others that may exist at the GUT or Planck scale simply become too weak to detect in the realm we can observe, with one exception: gravity, whose exceedingly weak interaction is magnified by the presence of the enormous masses of stars and planets." Wikipedia
