The Pound-Rebka experiment is between two static LNIFS.
Jefferson laboratory at Harvard University. The experiment occurred in the left "tower". The attic was later extended in 2004.
http://en.wikipedia.org/wiki/Pound–Rebka_experiment
Einstein's gravity redshift from the Sun uses
dt = ds(emit)/(1 - rs/r(emit))^1/2 = ds'(absorb)/(1 - rs/r(absorb))^1/2
f(absorb)/(1 - rs/r(emit))^1/2 = f(emit)/(1 - rs/r(absorb))^1/2
f(absorb) = f(emit)(1 - rs/r(emit))^1/2 /(1 - rs/r(absorb))^1/2
rs << r(emit)
rs << r(absorb)
f(absorb) ~ f(emit)(1 - rs/2r(emit)) (1 + rs/2r(absorb))
~ f(emit)(1 + (rs/2)(1/r(absorb) - 1/r(emit)))
~ f(emit)(1 + (rs/2r(emit))(r(emit)/r(absorb) - 1)
However, in the case of observation of the Sun
r(emit)/r(absorb) ~ 10^11/10^13 = 10^-2
therefore with ~ 1% error
f(absorb) ~ f(emit)(1 + (rs/2r(emit))(10^-2 - 1) ~ f(emit)(1 - .99(rs/2r(emit)) ~ f(emit)(1 - .99(10^5/10^13) ~ f(emit)(1 - .99x10^-8)
so we see that the gravity redshift on spectral lines emitted from the surface of the Sun to Earth is only of order 10^-8, i.e. megaHz for visible light.
The Earth is on geodesic orbit in the curvature field of the Sun. So there are two more approximations here.
Even though the Earth is LIF in the Sun's curvature field we approximate it it like a static LNIF. Note that a static LNIF becomes LIF as r ---> infinity. We see that this approximation only makes a 1% error in the coefficient of the major contribution to the shift of 10^-8.
We also neglect the covariant acceleration of the detector on Earth's surface of g ~ 10 meters/sec^2 in the curvature field of the Earth.
Note that the curvature field of the Sun at Earth is of order 10^5/(10^13)^3 cm^-2 ~ 10^-34cm^-2 i.e. curvature radius of 10^17 cm.
The curvature field of the Earth at the surface of Earth is of order 1/(10^9)^3 ~ 10^-27 cm^-2, i.e. curvature radius of ~ 10^13 cm.
One can do a simple experiment at the space station to test all this in a new way and detect horizon complementarity - more on this another time.
On Jan 28, 2011, at 7:31 PM, JACK SARFATTI wrote:
Your problem Z is that you simply do not look at the diagram.
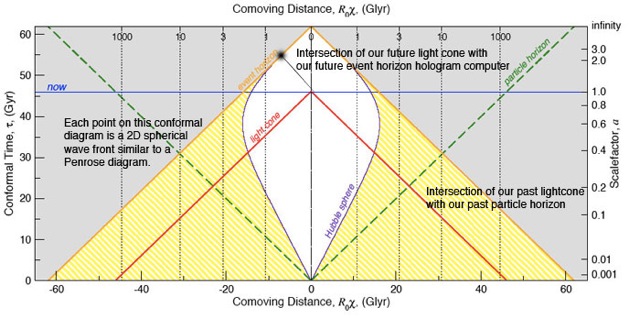
Pick any vertical (constant co-moving coord) world line you like. The Copernican principle is obeyed.
Its past particle horizon is its future light cone at a(0) = 0. Retarded light in our past cone from the past particle horizon is infinitely redshifted.
Light rays at 45deg & 135 deg on this conformal diagram.
Its future event horizon is its past light cone at a(infinity) = infinity. Advanced light from this horizon back to us at r = 0 is infinitely redshifted, but retarded light from r = 0 to it is infinitely blue shifted (classically).
Here t = proper metric time not the conformal time tau.
1) assume only retarded light signals.
Therefore, we only detect at a point stuff on the past light cone of that point.
2) Now we have a choice.
2a) the future horizon is not a total absorber, so we can see retarded signals from Galaxy X even when we are beyond Galaxy X's future event horizon.
2b) the future horizon is a Wheeler-Feynman total absorber from the real electron-positron plasma therefore no light rays from r = 0 make it past its future horizon. In that case, and only that case is Nick right in one of his statements. Only photons emitted from r = 0 see the plasma at their horizon r = /\^-1/2. LIFs do not see it. The blue shifted photon relative to the LNIF virtual electron-positron pairs clamped to the the r = /\^-1/2 horizon (of thickness Lp) provides the energy needed to pull them out of the vacuum in accord with the Unruh temperature T(r) = hg(r)/ckB.
Again that's horizon complementarity.
Nick is mistaken that a retarded photon from r = 0 is infinity redshifted. In fact, its the opposite, its infinitely blue shifted for a static LNIF detector clamped to the horizon. Not so for a co-moving detector because of horizon complementarity. Basically the co-moving detector in de Sitter space has acceleration 0, i.e. LIF, but a static LNIF detector has acceleration g(r) = 2c^2/\r(1 - /\r^2)^-1/2 ---> 0 at r = 0 and ---> infinity (classically) at r = /\^-1/2.
Also the frequency shift is
f(r) = f(0)(1 - /\r^2)^-1/2
