On Jun 29, 2011, at 3:01 PM, Ruth Elinor Kastner wrote:
Jack: I remember discussing this with John Cramer a few years ago. I found a reference (by Shih et al as I recall) saying that you cannot get an interference pattern without coincidence of the two photons -- this what Cramer refers to not seeing in the Dopfer thesis. Without coincidence you just get noise. I think this is the reason it might be impossible to get signalling. If one is able to improve the resolution of the down-conversion process so that you can see the interference pattern independently, then my understanding is that you lose the EPR correlation. Apologies if someone has already mentioned this and I missed it.
Ruth
Yes, that is the standard argument I am very familiar with. However, now Cramer recently claims he can get the interference pattern without the coincidence circuit because of advances in EPR sources. According to a document that Russell Targ sent me, Cramer now claims that, with the proper source of EPR pairs switching off the coincidence circuit is only a 15% reduction in receiver fringe visibility if the Heisenberg microscope is switched off at the transmitter. This clearly violates Stapp's et-al's general proof to the contrary within OQT.
I claim I have carried out Stapp's linear unitary partial trace of the EPR pair reduced density matrix proof in this particular situation in David Kaiser's Fig 9.1 of The Hippies Who Saved Physics:
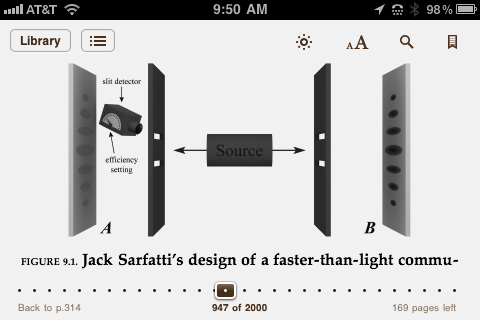
And that the implicit assumption in his general partial trace of the EPR pair density matrix proof in the situation of Fig 9.1 is my
(A1|A2) = 0
i.e. orthogonality of the slit states on the transmitter side. So that is the issue here.
(There is a glitch in the Joomla program that screws up the equations. I am trying to fix it.)
Where is the precise error in my algebraic analysis of Kaiser's Fig 9.1 above?
________________________________________
From: Jack Sarfatti [
Sent: Wednesday, June 29, 2011 4:11 PM
To: art wagner
Subject: Re: Quantum Mechanics 1: The No-FTL signalling theorem
The paper looks good. However my algebra is very simple. The issue is whether it contains an obvious contradiction with OQT? Even a smart undergrad physics major should be able to point out the error if indeed there is one.
I claim (A1|A2) = 0
Is necessary to get no signal in that instance for Kaiser's Fig 9.1. So far neither Henry nor any other quantum mechanic has actually addressed the relevant point.
On Jun 29, 2011, at 12:58 PM, art wagner > wrote:
Could the viewpoint espoused by this paper on the nature of the wavefunction be of any use here? [I do realize you're using bra-ket forms] - http://arxiv.org/ftp/arxiv/papers/1001/1001.5085.pdf
________________________________
Date: Wed, 29 Jun 2011 12:44:58 -0700
From:
Subject: Re: Quantum Mechanics 1: The No-FTL signalling theorem
Henry
I certainly agree that changing the statistical rules of OQT will allow signal nonlocality as in Antony Valentini's papers that are clearly sufficient, but is it necessary? John Cramer has recently suggest it is not necessary.
At this point I am playing Devil's Advocate. I expect my algebra has an error, but I have not been able to get you to really address that particular alleged counter example to your general proof. My model is essentially similar to John Cramer's variation on the Dopfur experiment.
I wrote several lines of algebra. Which ones do you disagree with as a description of Kaiser's Fig 9.1.
:-)
________________________________
From: Henry P. Stapp >;
To: JACK SARFATTI >;
Subject: Quantum Mechanics 1: The No-FTL signalling theorem
Sent: Wed, Jun 29, 2011 5:18:04 PM
Since you seem to be contemplating producing faster-than-light signalling by merely choosing unusual experiments conditions, but not changing the basic statistical rules of orthodox QM, and seem to have doubts the correctness of the No-FTL-Signalling Theorem, it might be instructive to look again at the usual derivation.
The basic interpretive rule of OQM is that the probability that a measurement associated with a projection operator P will give the positive outcome "Yes" is
The basic interpretive rule of OQM is that the probability that a measurement associated with a projection operator P will give the
positive outcome "Yes" is
(P)= Trace P rho/Trace rho
and that this "Yes" response to the probing action will reduce the
prior state rho to (P rho P)/trace P rho P.
The probability of the negative response "No" is
(P') = Trace P' rho/ Trace rho, with P'= (I-P).
Thus the probability of "Yes" plus the probability of "No" is
(Trace P rho/Trace rho)+ (Trace (I-P) rho/Trace rho)
=Trace (P + I - P)/Trace rho
= 1.
If Q is a projection operator whose support is spacelike
separated from the support of P, so that QP=PQ,
then the probability of "Yes" for Q and "Yes" for P is
(QP) = Trace QP rho/Trace rho
and the probability for "Yes" for Q and "No" for P is
(QP') = Trace Q(I-P) rho/ Trace rho.
Hence the probability of Yes for Q if the outcome of the mearurement
of P is unknown is
(QP) + (QP')
which is just
(Q):
This does not depend upon which measurement P was performed in the
faraway region: different choices of P produce no effect on the
probability of the outcome of the measurement in the region
associated with Q.
I do not see how this result can be rationally challenged,
given the standard rules of OQT.
Given any finite set of kets {|A1), |A2), ... , |AN)}
orthogonal or not, any non zero ket
|X) = c1|A1) + c2|A2) + ... CN|AN),
with complex coefficients Ci,
gives a projection operator
P= |X)(X|/(X|X)
(PP= P)
I do not see how anyone can rationally challenge these
conclusions, given the rules of OQT. They imply that,
given the rules of OQT, the probabilities of outcomes
on either side of Sarfatti's (or anyone's) experiment cannot
depend on which experiment is performed in the faraway other
region: a sender cannot, by his free choosings of which measurement
P to perform in L, send a message to a colleague that is observing the outcome of a measurement of Q in a region R that is spacelike separated from L: no matter what Q is measured in L, the outcome
predicted by OQT will be independent of which P the "sender" chooses.
Thus sending a FTL signal requires no mere clever choices of complex
measurements P and Q: it requires also a violation of the laws of OQT.
I have no doubt that this very simple, but extremely important, fact was known to the founders of quantum theory.
