

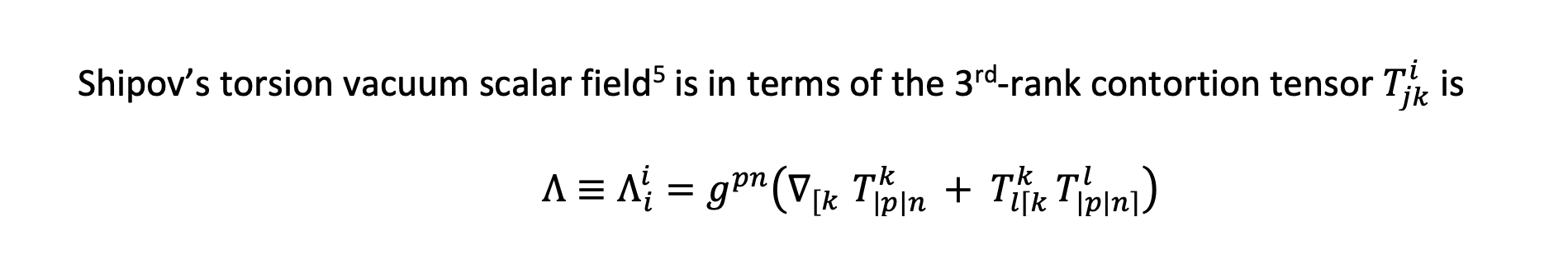

whose origin moves on a timelike geodesic determined by the translational symmetric Levi-Civita metric (Christoffel symbols). This is an additional torsion field contribution to geodesic frame drag that is already seen even when the torsion field is zero as shown most intuitively in Kip Thorne’s papers[i] showing the electromagnetic analog structures of Einstein’s 1916 purely translational vacuum Weyl piece of the Riemann-Curvature tensor.
When one splits spacetime into space plus time, the Weyl curvature tensor (vacuum Riemann tensor) gets split into two spatial, symmetric, and trace-free (STF) tensors: (i) the Weyl tensor's so-called "electric" part or tidal field, and (ii) the Weyl tensor's so-called "magnetic" part or frame-drag field. Being STF, the tidal field and frame-drag field each have three orthogonal eigenvector fields which can be depicted by their integral curves.
From the local gauge point of view, Einstein’s 1916 metric theory is simply the local gauge field from the 4 translations. The covariant curl of this Levi-Civita-Christoffel non-tensor metric connection corresponds to disclination defects in parallel transport of tensors using the connection around closed loops in the tangent fiber space. Beyond Einstein 1916 locally gauging the 6 space-time rotations of the Lorentz group of 1905 special relativity gives the antisymmetric tensor torsion field connection corresponding dislocation defects in which attempt to make a closed loop in the tangent space using the larger connection for parallel transport fails leaving an open gap.
One can go one step further and locally gauge the 4 conformal boosts and the 1 dilation generator of Roger Penrose’s 15 parameter “twistor” subgroup of GL(4,R) to get a non-metricity piece of the total connection in extended alternative gravity theory beyond 1916 GR.
[i] Visualizing Spacetime Curvature via Frame-Drag Vortexes and Tidal Tendexes I. General Theory and Weak-Gravity Applications
Authors: David A. Nichols, Robert Owen, Fan Zhang, Aaron Zimmerman, Jeandrew Brink, Yanbei Chen, Jeffrey D. Kaplan, Geoffrey Lovelace, Keith D. Matthews, Mark A. Scheel, Kip S. Thorne
Abstract: When one splits spacetime into space plus time, the Weyl curvature tensor (vacuum Riemann tensor) gets split into two spatial, symmetric, and trace-free (STF) tensors: (i) the Weyl tensor's so-called "electric" part or tidal field, and (ii) the Weyl tensor's so-called "magnetic" part or frame-drag field. Being STF, the tidal field and frame-drag field each have three orthogonal eigenvector fields which can be depicted by their integral curves. We call the integral curves of the tidal field's eigenvectors tendex lines, we call each tendex line's eigenvalue its tendicity, and we give the name tendex to a collection of tendex lines with large tendicity. The analogous quantities for the frame-drag field are vortex lines, their vorticities, and vortexes. We build up physical intuition into these concepts by applying them to a variety of weak-gravity phenomena: a spinning, gravitating point particle, two such particles side by side, a plane gravitational wave, a point particle with a dynamical current-quadrupole moment or dynamical mass-quadrupole moment, and a slow-motion binary system made of nonspinning point particles. [Abstract is abbreviated; full abstract also mentions additional results.]
https://arxiv.org/abs/1108.5486
Visualizing Spacetime Curvature via Frame-Drag Vortexes and Tidal Tendexes II. Stationary Black Holes
Authors: Fan Zhang, Aaron Zimmerman, David A. Nichols, Yanbei Chen, Geoffrey Lovelace, Keith D. Matthews, Robert Owen, Kip S. Thorne
Abstract: When one splits spacetime into space plus time, the Weyl curvature tensor (which equals the Riemann tensor in vacuum) splits into two spatial, symmetric, traceless tensors: the tidal field E, which produces tidal forces, and the frame-drag field B, which produces differential frame dragging. In recent papers, we and colleagues have introduced ways to visualize these two fields: tidal tendex lines (integral curves of the three eigenvector fields of E) and their tendicities (eigenvalues of these eigenvector fields); and the corresponding entities for the frame-drag field: frame-drag vortex lines and their vorticities. These entities fully characterize the vacuum Riemann tensor. In this paper, we compute and depict the tendex and vortex lines, and their tendicities and vorticities, outside the horizons of stationary (Schwarzschild and Kerr) black holes; and we introduce and depict the black holes' horizon tendicity and vorticity (the normal-normal components of E and B on the horizon). For Schwarzschild and Kerr black holes, the horizon tendicity is proportional to the horizon's intrinsic scalar curvature, and the horizon vorticity is proportional to an extrinsic scalar curvature. We show that, for horizon-penetrating time slices, all these entities (E, B, the tendex lines and vortex lines, the lines' tendicities and vorticities, and the horizon tendicities and vorticities) are affected only weakly by changes of slicing and changes of spatial coordinates, within those slicing and coordinate choices that are commonly used for black holes. https://arxiv.org/abs/1208.3034
Visualizing Spacetime Curvature via Frame-Drag Vortexes and Tidal Tendexes III. Quasinormal Pulsations of Schwarzschild and Kerr Black Holes
Authors: David A. Nichols, Aaron Zimmerman, Yanbei Chen, Geoffrey Lovelace, Keith D. Matthews, Robert Owen, Fan Zhang, Kip S. Thorne
Abstract: In recent papers, we and colleagues have introduced a way to visualize the full vacuum Riemann curvature tensor using frame-drag vortex lines and their vorticities, and tidal tendex lines and their tendicities. We have also introduced the concepts of horizon vortexes and tendexes and 3-D vortexes and tendexes (regions where vorticities or tendicities are large). Using these concepts, we discover a number of previously unknown features of quasinormal modes of Schwarzschild and Kerr black holes. These modes can be classified by mode indexes (n,l,m), and parity, which can be electric [(-1)^l] or magnetic [(-1)^(l+1)]. Among our discoveries are these: (i) There is a near duality between modes of the same (n,l,m): a duality in which the tendex and vortex structures of electric-parity modes are interchanged with the vortex and tendex structures (respectively) of magnetic-parity modes. (ii) This near duality is perfect for the modes' complex eigenfrequencies (which are well known to be identical) and perfect on the horizon; it is slightly broken in the equatorial plane of a non-spinning hole, and the breaking becomes greater out of the equatorial plane, and greater as the hole is spun up; but even out of the plane for fast-spinning holes, the duality is surprisingly good. (iii) Electric-parity modes can be regarded as generated by 3-D tendexes that stick radially out of the horizon. As these "longitudinal," near-zone tendexes rotate or oscillate, they generate longitudinal-transverse near-zone vortexes and tendexes, and outgoing and ingoing gravitational waves. The ingoing waves act back on the longitudinal tendexes, driving them to slide off the horizon, which results in decay of the mode's strength. (iv) By duality, magnetic-parity modes are driven in this same manner by longitudinal, near-zone vortexes that stick out of the horizon. https://arxiv.org/abs/1208.3038



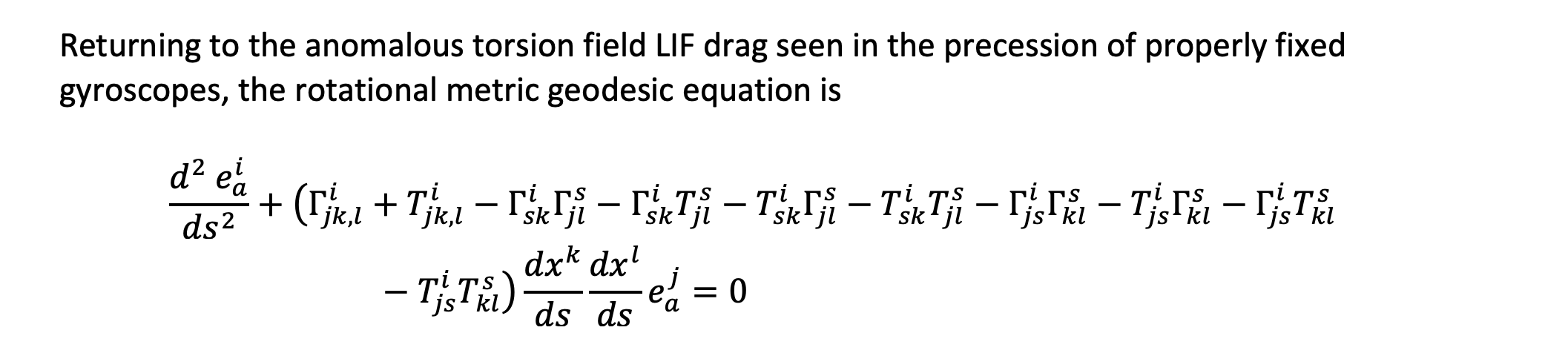


 Stay tuned.
Stay tuned.
