{tex}\[G_{\mu \nu } + kT_{\mu \nu } = 0\]{/tex}
Einstein's 1916 GR gravity curvature field - matter field source field equations
"While there are many excellent expositions of general relativity, few adequately explain the geometrical meaning of the basic equation of the theory: Einstein's equation. Here we give a simple formulation of this equation in terms of the motion of freely falling test particles." - John Baez
the intrinsic structure is all in the force-free timelike and null geodesics - Newton's gravity force is a chimera a wrong turn in the road to reality - the real meaning of the equivalence principle! Newton's gravity force is off-geodesic i.e. contingent not of fundamental local objective importance
F = - GMm/r^2 (Newton's gravity force = 100% inertial force)
only for static LNIFs in a SSS metric field
Newton's 17th Century gravity force is not fundamental!
Beware naively trying to unify it with EM-Weak-Strong Forces.
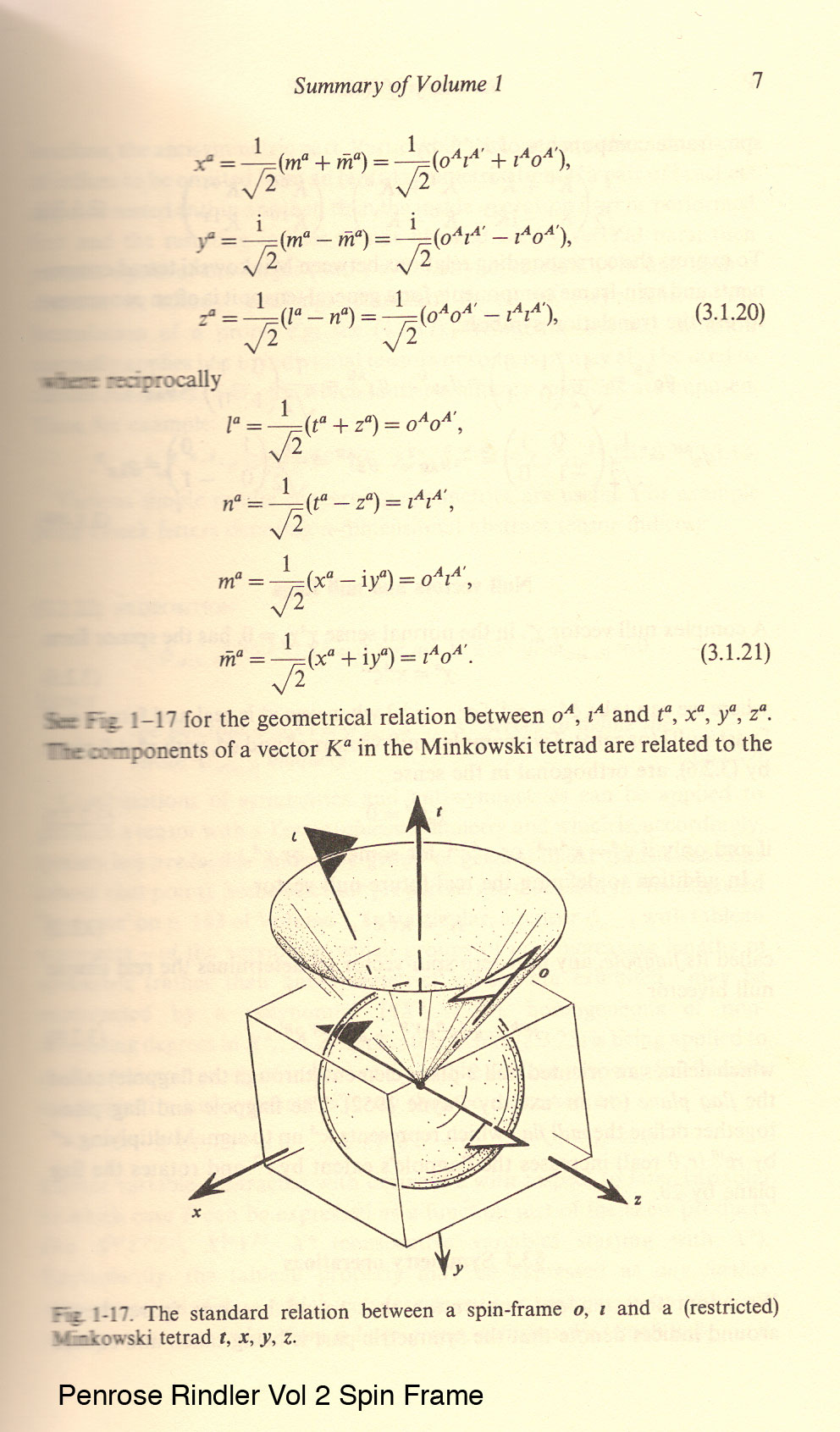
The spin 1 "square root" gravity tetrad fields describe the geodesic test particles - they are Bell entangled pair states of 2-spinor light cone qubits for the timelike geodesics x,y,z,t (3.1.20) and they are unentangled for the null geodesic light rays l,n,m & m* (3.1.21) Penrose-Rindler below:
note t ~ (oo + ii) not shown below it's on p. 6 of Penrose & Rindler Vol 2
Testing new Joomla plug in to show math formulas properly.
Attempt to write Aharonov's equation for weak measurement expectation value - Math Text --> Joomla does not properly translate.
2nd try
{tex}\[\left\langle {\bar A} \right\rangle _w \equiv \frac{1}{N}\sum\limits_{i = 1}^N {\left\langle {A^{\left( i \right)} } \right\rangle _w } = \frac{1}{N}\sum\limits_{i = 1}^N {N_i } \frac{{\left\langle i \right|A\left| \psi \right\rangle }}{{\left\langle i \right|\left. \psi \right\rangle }}\mathop \to \limits_{N \to \infty } \left\langle \psi \right|A\left| \psi \right\rangle\]{/tex}
Got it.
