The quantum mechanics of time travel through post-selected teleportation

Seth Lloyd1, Lorenzo Maccone1, Raul Garcia-Patron1, Vittorio Giovannetti2, Yutaka Shikano1,3 wrote
"Einstein’s theory of general relativity allows the existence
of closed timelike curves, paths through spacetime
that, if followed, allow a time traveler – whether human
being or elementary particle – to interact with her former
self. ...
This paper explores a particular
version of closed timelike curves based on combining
quantum teleportation with post-selection. The resulting
post-selected closed timelike curves (P-CTCs) provide
a self-consistent picture of the quantum mechanics
of time-travel. ...
As in
all versions of time travel, closed timelike curves embody
apparent paradoxes, such as the grandfather paradox, in
which the time traveller inadvertently or on purpose performs
an action that causes her future self not to exist.
Einstein (a good friend of G¨odel) was himself seriously
disturbed by the discovery of CTCs [11]. Because the
theory of P-CTCs rely on post-selection, they provide
self-consistent resolutions to such paradoxes: anything
that happens in a P-CTC can also happen in conventional
quantum mechanics with some probability. Similarly, the
post-selected nature of P-CTCs allows the predictions
and retrodictions of the theory to be tested experimentally,
even in the absence of an actual general-relativistic
closed timelike curve. ...
The G¨odel universe consists of a cloud of
swirling dust, of sufficient gravitational power to support
closed timelike curves. Later, it was realized that closed
timelike curves are a generic feature of highly curved, rotating
spacetimes: the Kerr solution for a rotating black
hole contains closed timelike curves within the black hole
horizon; and massive rapidly rotating cylinders typically
are associated with closed timelike curves [2, 8, 12]. The
topic of closed timelike curves in general relativity continues
to inspire debate: Hawking’s chronology protection
postulate, for example, suggests that the conditions
needed to create closed timelike curves cannot arise in
any physically realizable spacetime ...
Hartle and Politzer pointed out that in the presence
of closed timelike curves, the ordinary correspondence
between the path-integral formulation of quantum
mechanics and the formulation in terms of unitary evolution
of states in Hilbert space breaks down [5, 7]. Morris
et al. explored the quantum prescriptions needed to construct
closed timelike curves in the presence of wormholes,
bits of spacetime geometry that, like the handle
of a coffee cup, ‘break off’ from the main body of
the universe and rejoin it in the the past [4]. Meanwhile,
Deutsch formulated a theory of closed timelike
curves in the context of Hilbert space, by postulating
self-consistency conditions for the states that enter and
exit the closed timelike curve ...
Quantum mechanics supports a variety
of counter-intuitive phenomena which might allow
time travel even in the absence of a closed timelike curve
in the geometry of spacetime. ...
We start from the prescription that time travel
effectively represents a communication channel from the
future to the past. ...
A well-known quantum communication channel is
given by quantum teleportation, in which shared entanglement
combined with quantum measurement and classical
communication allows quantum states to be transported
between sender and receiver. We show that if
quantum teleportation is combined with post-selection,
then the result is a quantum channel to the past. The entanglement
occurs between the forward- and backward going
parts of the curve, and post-selection replaces the
quantum measurement and obviates the need for classical
communication, allowing time travel to take place. ...
entanglement and projection can give rise to closed timelike
curves ...
Deutsch’s theory has recently
been critiqued by several authors as exhibiting
self-contradictory features [33–36]. By contrast, although
any quantum theory of time travel quantum mechanics
is likely to yield strange and counter-intuitive results,
P-CTCs appear to be less pathological [17]. They are
based on a different self-consistent condition that states
that self-contradictory events do not happen (Novikov
principle [29]). ...
Pegg points out that this can arise because
of destructive interference of self-contradictory histories
[22]. ...
in addition to
general-relativistic CTCs, our proposed theory can also
be seen as a theoretical elaboration of Wheeler’s assertion
to Feynman that ‘an electron is a positron moving
backward in time’ [16]. In particular, any quantum
theory which allows the nonlinear process of postselection
supports time travel even in the absence of general relativistic
closed timelike curves.
The mechanism of P-CTCs [17] can be summarized by
saying that they behave exactly as if the initial state of
the system in the P-CTC were in a maximal entangled
state (entangled with an external purification space) and
the final state were post-selected to be in the same entangled
state. When the probability amplitude for the transition
between these two states is null, we postulate that
the related event does not happen (so that the Novikov
principle [29] is enforced). ...
Note that Deutsch’s
formulation assumes that the state exiting the CTC in
the past is completely uncorrelated with the chronologypreserving
variables at that time: the time-traveler’s
‘memories’ of events in the future are no longer valid.
The primary conceptual difference between Deutsch’s
CTCs and P-CTCs lies in the self-consistency condition
imposed. ...
It seems that, based on what is currently known on
these two approaches, we cannot conclusively choose PCTCs
over Deutsch’s, or vice versa. Both arise from
reasonable physical assumptions and both are consistent
with different approaches to reconciling quantum mechanics
with closed timelike curves in general relativity.
A final decision on which of the two is “actually the case”
may have to be postponed to when a full quantum theory
of gravity is derived (which would allow to calculate
from first principles what happens in a CTC) or when
a CTC is discovered that can be tested experimentally. ...
[Aharonov's theory]
Here we briefly comment on the two-state vector formalism
of quantum mechanics [48, 51]. It is based on
post-selection of the final state and on renormalizing the
resulting transition amplitudes: it is a time-symmetrical
formulation of quantum mechanics in which not only the
initial state, but also the final state is specified. As such,
it shares many properties with our post-selection based
treatment of CTCs. In particular, in both theories it
is impossible to assign a definite quantum state at each
time: in the two-state formalism the unitary evolution
forward in time from the initial state might give a different
mid-time state with respect to the unitary evolution
backward in time from the final state. Analogously
in a P-CTC, it is impossible to assign a definite state
to the CTC system at any time, given the cyclicity of
time there ...
Another aspect that the two-state
formalism and P-CTCs share is the nonlinear renormalization
of the states and probabilities. In both cases this
arises because of the post-selection. In addition to the
two-state formalism, our approach can also be related to
weak values [48, 52], since we might be performing measurements
between when the system emerges from the
CTC and when it re-enters it. Considerations analogous
to the ones presented above apply. It would be a mistake,
however, to think that the theory of post-selected closed
timelike curves in some sense requires or even singles out
the weak value theory. Although the two are compatible
with each other, the theory of P-CTCs is essentially
a ‘free-standing’ theory that does not give preference to
one interpretation of quantum mechanics over another. ...
the non-unitarity comes from the fact that, after the CTC is
closed, for the chronology-respecting system it will be forever
inaccessible. The nonlinearity of (9) is more difficult
to interpret, but is connected with the periodic boundary
conditions in the CTC. ...
when quantum fields inside a CTC interact with
external fields, linearity and unitarity is lost. ...
Hartle notes
that CTCs might necessitate abandoning not only unitarity
and linearity, but even the familiar Hilbert space
formulation of quantum mechanics [7]. Indeed, the fact
that the state of a system at a given time can be written
as the tensor product states of subsystems relies crucially
on the fact that operators corresponding to spacelike
separated regions of spacetime commute with each
other. When CTCs are introduced, the notion of ‘spacelike’
separation becomes muddied. The formulation of
closed timelike curves in terms of P-CTCs shows, however,
that the Hilbert space structure of quantum mechanics
can be retained. ...
any quantum theory that allows the nonlinear
process of projection onto some particular state, such
as the entangled states of P-CTCs, allows time travel
even when no spacetime closed timelike curve exists. ...
projection is a non-linear process that cannot be implemented deterministically
in ordinary quantum mechanics, it can easily be implemented in a probabilistic fashion.
Consequently,  the effect of P-CTCs can be tested simply by
performing quantum teleportation experiments, and by
post-selecting only the results that correspond to the desired
entangled-state output. ...
it might be possible
to implement time travel even in the absence of a
general-relativistic closed timelike curve. The formalism
of P-CTCs shows that such quantum time travel can be
thought of as a kind of quantum tunneling backwards
in time, which can take place even in the absence of a
classical path from future to past. ...
It has been long known that nonlinear quantum mechanics
potentially allows the rapid solution of hard problems
such as NP-complete problems [56]. The nonlinearities
in the quantum mechanics of closed timelike
curves is no exception ...

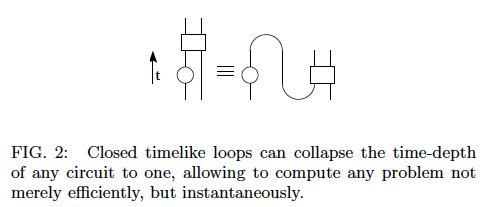
Bennett et al. argue, the programmer who is using a
Deutschian closed timelike
curve as part of her quantum computer typically finds
the output of the curve is completely decorrelated from
the problem she would like to solve: the curve emits random
states.
In contrast, because P-CTCs are formulated explicitly
to retain correlations with chronology preserving curves,
quantum computation using P-CTCs do not suffer from
state-preparation ambiguity. That is not so say that PCTCs
are computationally innocuous: their nonlinear
nature typically renormalizes the probability of states in
an input superposition, yielding to strange and counterintuitive
effects. For example, any CTC can be used
to compress any computation to depth one, as shown
in Fig. 2. Indeed, it is exactly the ability of nonlinear
quantum mechanics to renormalize probabilities from
their conventional values that gives rise to the amplification
of small components of quantum superpositions
that allows the solution of hard problems. Not least
of the counter-intuitive effects of P-CTCs is that they
could still solve hard computational problems with ease!
The ‘excessive’ computational power of P-CTCs is effectively
an argument for why the types of nonlinearities
that give rise to P-CTCs, if they exist, should only
be found under highly exceptional circumstances such as
general-relativistic closed timelike curves or black-hole
singularities. ...
We have extensively argued that P-CTCs are physically
inequivalent to Deutsch’s CTCs. In Sec. II we
showed that P-CTCs are compatible with the pathintegral
formulation of quantum mechanics. This formulation
is at the basis of most of the previous analysis
of quantum descriptions of closed time-like curves, since
it is particularly suited to calculations of quantum mechanics
in curved space time. P-CTCs are reminiscent of,
and consistent with, the two-state-vector and weak-value
formulation of quantum mechanics. It is important to
note, however, that P-CTCs do not in any sense require
such a formulation. ...
we have argued that, as Wheeler’s picture
of positrons as electrons moving backwards in time suggests,
P-CTCs might also allow time travel in spacetimes
without general-relativistic closed timelike curves. If nature
somehow provides the nonlinear dynamics afforded
by final-state projection, then it is possible for particles
(and, in principle, people) to tunnel from the future to
the past.
Finally, in Sec. V we have seen that P-CTCs are computationally
very powerful, though less powerful than the
Aaronson-Watrous theory of Deutsch’s CTCs.
Our hope in elaborating the theory of P-CTCs is that
this theory may prove useful in formulating a quantum
theory of gravity, by providing new insight on one of the
most perplexing consequences of general relativity, i.e.,
the possibility of time-travel."